Binary classification evaluation in R via ROCR

A binary classifier makes decisions with confidence levels. Usually it’s imperfect: if you put a decision threshold anywhere, items will fall on the wrong side — errors. I made this a diagram a while ago for Turker voting; same principle applies for any binary classifier.

So there are a zillion ways to evaluate a binary classifier. Accuracy? Accuracy on different item types (sens, spec)? Accuracy on different classifier decisions (prec, npv)? And worse, over the years every field has given these metrics different names. Signal detection, bioinformatics, medicine, statistics, machine learning, and more I’m sure. But in R, there’s the excellent ROCR package to compute and visualize all the different metrics.

I wanted to have a small, easy-to-use function that calls ROCR and reports the basic information I’m interested in. For preds, a vector of predictions (as confidence scores), and labels, the true labels for the instances, it works like this:

> binary_eval(preds, labels)

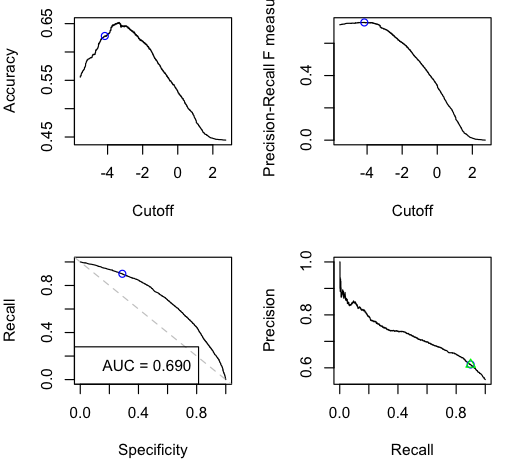
These are four graphs showing variation of classifier performance as the cutoff changes. There’s more than one because they convey different, interesting information. There are four because then they arrange nicely into a square. I wanted to balance having enough information vs. simplicity. The graphs are:

The other thing binary_eval does is show one cutoff point across all the graphs — the blue circle — and display its associated performance metrics. So here, it used the naive cutoff (0 for real-valued predictions; 0.5 for probabilities) and plotted that point with the blue circle on all the graphs. Plus it reports for that cutoff:

Predictions seem to be real-valued scores, so using naive cutoff 0:
Acc = 0.531
  F = 0.338
 Prec = 0.780
  Rec = 0.216
 Spec = 0.924
Balanced Acc = 0.570

So it’s very apparent that the naive cutoff isn’t performing well here. We can call it and supply a cutoff, or perhaps better, ask it to pick a cutoff that maximizes any metric that ROCR knows about. For example, calibration for accuracy or F-score:

binary_eval(preds, labels, ‘acc’)	binary_eval(preds, labels, ‘f’)

I added the function to my R utilities file, here: dlanalysis/util.R.

Some people in machine learning like to use standalone programs like PERF to compute all these metrics. R is better if you know it. You can calculate all sorts of things with it. Above I was using R for the evaluation of the outputs of a command-line classifier, importing them easily with scan() and scan(pipe(“cut -f1 < data.svmlight_format”)).

The best Wikipedia page to start reading about the zillions of all of these interrelated confusion matrix metrics might be the the ROC page.

If you want to see lots and lots more evaluation metrics, look at the “extended classifier evaluation” section of LingPipe’s sentiment analysis tutorial. And once you get into multiclass and such, all complexity hell breaks loose.