This confused me for a while when I first learned it, so in case it helps anyone else:
The logistic sigmoid function, a.k.a. the inverse logit function, is
\[ g(x) = \frac{ e^x }{1 + e^x} \]
Its outputs range from 0 to 1, and are often interpreted as probabilities (in, say, logistic regression).
The tanh function, a.k.a. hyperbolic tangent function, is a rescaling of the logistic sigmoid, such that its outputs range from -1 to 1. (There’s horizontal stretching as well.)
\[ tanh(x) = 2 g(2x) - 1 \]
It’s easy to show the above leads to the standard definition \( tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}} \). The (-1,+1) output range tends to be more convenient for neural networks, so tanh functions show up there a lot.
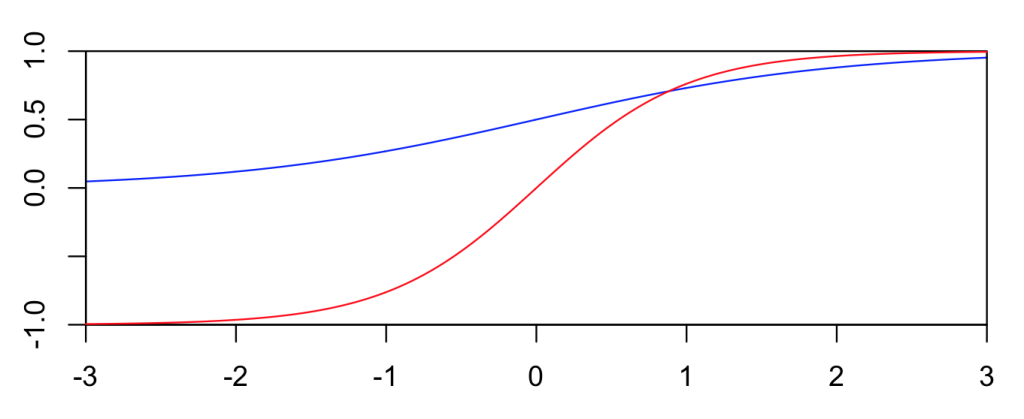
The two functions are plotted below. Blue is the logistic function, and red is tanh.