I love dinosaur comics. What a quicker way to learn philosophy than reading all those books.
For example:
Now I have an opinion on verificationism! I like the yellow dinosaur better. Scientific empiricism is great, dithering about strict notions of meaning, not so great. See, isn’t epistemology easy?
There’s a company, Emotiv, that’s building an EEG interface for the game systems. Any company with a science-fiction-y vision statement sounds like a good time to me:
Communication between man and machine has always been limited to conscious interaction, with non-conscious communication — expression, intuition, perception — reserved solely for the human realm. At Emotiv, we believe that future communication between man and machine will not only be limited to the conscious communication that exists today, but non-conscious communication will play a significant part.
Our mission is to create the ultimate interface for the next-generation of man-machine interaction, by evolving the interaction between human beings and electronic devices beyond the limits of conscious interface. Emotiv is creating technologies that allow machines to take both conscious and non-conscious inputs directly from your mind.
They even have a cyborg-looking woman on the page.
Their claim is to detect emotion states of the player. Do you really need EEG for that? What about something less sexy like skin conductance? Facial expressions or more? I guess a big metal helmet detecting your brain must be inherently fun.
Along similar lines, the Internet has lots of advice on homemade EEG, with impressively detailed how-to instructions. Other sites seem to focus less on reading your brain’s outputs, and more on modifying its state/signals. For example, apparently you can hack your brain with an iPod. Sign me up, what I’ve always wanted.
(To be fair, here’s a more complete page on entrainment. The Emotiv link is from folks at neurodudes.)
I got nervous and panicky just reading about this game. I wonder if I could con some people into playing it.
Economics professors have a standard game they use to demonstrate how apparently rational decisions can create a disastrous result. They call it a “dollar auction.” The rules are simple. The professor offers a dollar for sale to the highest bidder, with only one wrinkle: the second-highest bidder has to pay up on their losing bid as well. Several students almost always get sucked in. The first bids a penny, looking to make 99 cents. The second bids 2 cents, the third 3 cents, and so on, each feeling they have a chance at something good on the cheap. The early stages are fun, and the bidders wonder what possessed the professor to be willing to lose some money.
The problem surfaces when the bidders get up close to a dollar. After 99 cents the last vestige of profitability disappears, but the bidding continues between the two highest players. They now realize that they stand to lose no matter what, but that they can still buffer their losses by winning the dollar. They just have to outlast the other player. Following this strategy, the two hapless students usually run the bid up several dollars, turning the apparent shot at easy money into a ghastly battle of spiraling disaster.
Theoretically, there is no stable outcome once the dynamic gets going. The only clear limit is the exhaustion of one of the player’s total funds. In the classroom, the auction generally ends with the grudging decision of one player to “irrationally” accept the larger loss and get out of the terrible spiral. Economists call the dollar auction pattern an irrational escalation of commitment. We might also call it the war in Iraq.
Is it ever rational to enter the game? What seems frightening is the aspect of losses — if you’re in the lead, any move by anyone else pushes you into the bad losing position of 2nd place.
Sometimes it seems bad countries come with long names. North Korea is “People’s Democratic Republic of Korea”, Libya is “Great Socialist People’s Libyan Arab Jamahiriya”, and the like. But on the other hand, there’s plenty of counter-examples — it’s the “United Kingdom of Great Britain and Northern Ireland” and “Republic of Cuba”, after all. Do long names with good-sounding adjectives correspond with non-democratic governments?
Fortunately, this can be tested. First, what words are out there? From the CIA Factbook’s data on long form names, here are some of the most popular words used by today’s countries, listed with the number of occurrences across all 194 names. I limited to tokens that appear >= 3 times. A majority of countries are Republics, while there are some Kingdoms, and even a few Democracies.
(146 of) (127 Republic) (17 Kingdom) (8 the) (8 Democratic) (6 State) (6 People’s) (5 United) (4 and) (4 Islamic) (4 Arab) (3 States) (3 Socialist) (3 Principality) (3 Islands) (3 Guinea) (3 Federal) (3 Commonwealth)
Now, we can group countries by included words and look at how democratic they are, as according to Freedom House‘s political rights scores. They look at a number of political freedoms — free elections, ability to run for office, power sharing, lack of military intervention in government, etc. to formulate the rating. The following chart shows the average political rights score per group of countries with the given word (actually, substring) in its name.
The upper rows show a substring and the number of names that are matched by it, and the average PR score. (These groups occasionally overlap.) The lower rows are several example countries for reference. So Republics are ever so slightly less democratic than your average non-Republic, and also amusingly, Kingdoms edge them out too. But Democratic, People’s, Socialist, Islamic and Arab countries are definitely the big-time un-democracies, while the only clear winners on the other side are Commonwealths and Principalities. Here are the members of the smaller groups:
Score Name /kingdom/ 1 Kingdom of Belgium 1 Kingdom of Denmark 1 Kingdom of the Netherlands 1 Kingdom of Norway 1 Kingdom of Spain 1 Kingdom of Sweden 1 United Kingdom of Great Britain and Northern Ireland 2 Kingdom of Lesotho 5 Kingdom of Tonga 5 Hashemite Kingdom of Jordan 5 Kingdom of Morocco 5 Kingdom of Bahrain 6 Kingdom of Bhutan 6 Kingdom of Cambodia 7 Kingdom of Thailand 7 Kingdom of Swaziland 7 Kingdom of Saudi Arabia /democ/ 2 Democratic Republic of Sao Tome and Principe 3 Democratic Republic of Timor-Leste 4 Democratic Socialist Republic of Sri Lanka 5 Federal Democratic Republic of Ethiopia 6 People's Democratic Republic of Algeria 5 Democratic Republic of the Congo 7 Lao People's Democratic Republic 7 Democratic People's Republic of Korea /state/ 1 Federated States of Micronesia 1 United States of America 1 State of Israel 2 Independent State of Samoa 2 United Mexican States 3 Independent State of Papua New Guinea 4 State of Kuwait 6 State of Qatar 7 State of Eritrea /feder/ 1 Federal Republic of Germany 1 Federated States of Micronesia 1 Swiss Confederation 2 Federative Republic of Brazil 4 Federal Republic of Nigeria 5 Federal Democratic Republic of Ethiopia 6 Russian Federation /people/ 4 People's Republic of Bangladesh 6 People's Democratic Republic of Algeria 7 People's Republic of China 7 Lao People's Democratic Republic 7 Great Socialist People's Libyan Arab Jamahiriya 7 Democratic People's Republic of Korea /arab/ 6 Arab Republic of Egypt 6 United Arab Emirates 7 Kingdom of Saudi Arabia 7 Syrian Arab Republic 7 Great Socialist People's Libyan Arab Jamahiriya /united/ 1 United Kingdom of Great Britain and Northern Ireland 1 United States of America 2 United Mexican States 4 United Republic of Tanzania 6 United Arab Emirates /islam/ 5 Islamic Republic of Mauritania 5 Islamic Republic of Afghanistan 6 Islamic Republic of Pakistan 6 Islamic Republic of Iran /commonwealth/ 1 Commonwealth of Australia 1 Commonwealth of The Bahamas 1 Commonwealth of Dominica /island/ 1 Republic of the Marshall Islands 4 Solomon Islands 6 Republic of the Fiji Islands /principality/ 1 Principality of Andorra 1 Principality of Liechtenstein 2 Principality of Monaco /social/ 4 Democratic Socialist Republic of Sri Lanka 7 Socialist Republic of Vietnam 7 Great Socialist People's Libyan Arab Jamahiriya
I just think it’s striking there’s such a small set of words used to describe countries, and that so many use “Republic”. It speaks to (some sort of) triumph of liberal politcal ideas that even the most dictatorial regimes have to at least pay lip service to them. This has certainly been going on for a while; I suppose names have been moving in this direction for a few hundred years.
I also looked at simple word lengths of country names. It’s not exactly the clearest bubbleplot ever, but if you go ahead and force a linear model (least-squares regression) on it, turns out each word contributes 0.26 points of un-democraticness. And if you viciously remove those lower right outliers (UK and Sao Tome), that coefficient bumps up to 0.39.
Boring details:
Standard problem: humans lived like crap for thousands and thousands of years, then suddenly some two hundred years ago dramatic industrialization and economic growth happened, though unevenly even through today. Here’s an interesting proposal to explain all this. Gregory Clark found startling empirical evidence that, in the time around the Industrial Revolution in England, wealthier families had more children than poorer families, while middle-class social values — non-violence, literacy, work ethic, high savings rates — also became more widespread during this time. According to the article at least, he actually seems to favor the explanation that human biological evolution was at work; though he notes cultural evolution is possible too. (That is, the children of wealthier families are socialized with their values; as the children of middle-class-valued families increase in proportion in society, the prevalence of those values increases too.)
In any case, the argument is that behavioral changes, not institutional changes, drove the rise of capitalism. I know that some people define institutions to include cultural norms (and therefore human behavior, right?), so I’m presuming that for Clark and the academic debates vaguely mentioned in the article, “institutions” means something more boring like government structure or enforcement of property rights. (I’m reading Samuel Bowles’s microeconomics book off and on, where he likes to mix behavioral and institutional ideas; and I seem to recall this from Avner Grief too; this all apparently is too confusing for me. (Bowles is quoted in the article.)) The article mentions Max Weber’s Protestant ethic as related to Clark in its being a behavioral thesis.
I’m awfully skeptical of biological evolution claims without any actual genetic evidence (though I quite like cultural evolutionary claims), but the theory is very neat and the archival data gathered is incredible, as you can see in this shamelessly ripped off diagram/explanation from the NYT article about the Clark’s book on this.
From an NYT Magazine article this Sunday, paraphrasing Isaiah Berlin:
The philosopher Isaiah Berlin once said that the trouble with academics and commentators is that they care more about whether ideas are interesting than whether they are true. Politicians live by ideas just as much as professional thinkers do, but they can’t afford the luxury of entertaining ideas that are merely interesting. They have to work with the small number of ideas that happen to be true and the even smaller number that happen to be applicable to real life. In academic life, false ideas are merely false and useless ones can be fun to play with. In political life, false ideas can ruin the lives of millions and useless ones can waste precious resources. An intellectual’s responsibility for his ideas is to follow their consequences wherever they may lead. A politician’s responsibility is to master those consequences and prevent them from doing harm.
I can’t speak for that level of politics, but I’ve seen in applied technology the distinction between interesting and true ideas can be great. (True in the sense of, it is true that the idea solves the problem at hand.) I’ve wasted plenty of time recently at work chasing down very interesting ideas only to reassess and do something more expedient. A different example from empirical science: it sure sounds interesting when the 1950′s Chomsky claims that language can’t be statistically modelled, though that turns out to be embarrassingly false.
Nice little NYT article on Martin Nowak, of evolution-of-cooperation fame. He’s the directory of Harvard’s Program for Evolutionary Dynamics which looks neat. I love the the Price Equation. Sweet.
This is fascinating — In China, you can get fined if you make a map of China without Taiwan or other disputed territories. Reminds me of being confused trying to find the primary airline of China.
Based of vague recollections of its name, I searched Google for {{ china air }}. The first hit was for China Airlines. But the second hit was Air China. The first is the state carrier of the ROC (Taiwan), the second is the PRC (mainland China). Turns out my intended concept, “Official Chinese airline”, isn’t a coherent concept if your political worldview includes both the ROC and PRC as entities. But maybe what I should have wanted was just airlines that fly around East Asia and various parts of China; in that case, getting both airlines is the right thing to do. At least Google got them both at the top of the list.
(p.s. anyone know how to force blogger to *not* destructively resize your images? sigh)
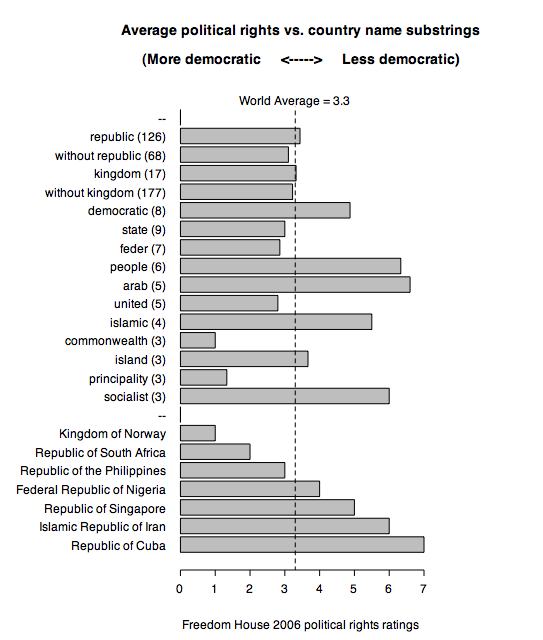
I think game theory could benefit immensely from better presentation. Its default presentation is pretty mathematical. This is good because it treats social interactions in an abstract way, highlighting their essential properties, but is bad because it’s hard to understand, especially at first.
However, I think I have a visualization that can sometimes capture the same abstract properties of the mathematics. Here’s a stab at using it to explain everyone’s favorite game, the prisoner’s dilemma.
THE PD: Two players each choose whether to play nice, or be mean — Cooperate or Defect. Then they simultaneously play their actions, and get payoffs depending on what both played. If both cooperated, they help each other and do well; if both defect, they do quite poorly. But if one tries to cooperate and the other defects, then the defector gets a big win, and the cooperator gets a crappy “sucker’s payoff”.
The formal PD definition looks like this:
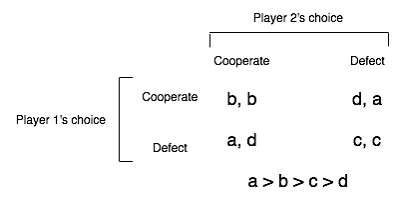
where each of the four pairs represents the (row player payoff, column player payoff) for that pair of choices. This 2×2 table, along with the constraint a>b>c>d, together capture all the properties outlined in the above paragraph. (There is usually one more constraint that a+d<2b but I'm dropping it for this discussion.) Usually it takes a few more paragraphs of prose to really explain things, but you're reading a blog and don't have patience for such silliness. Therefore the fun pictures.
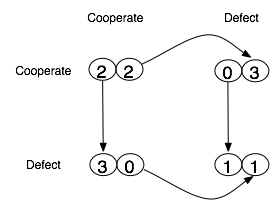
First, let’s look at the group level. Is there an outcome that makes everyone happy? Or at least, is there an outcome that’s incontrovertibly better compared to another outcome? Yes, actually. This relationship is true exactly one time. Here’s a new diagram that puts in example values for the payoffs:
The (C,C) outcome gets a payoff of 2 for each person, whereas the (D,D) payoff gets 1 for each person. Compared to DD, CC is better for everyone. This is called a Pareto improvement. Therefore there is an arrow drawn between them. The notation X
Y means that outcome Y is a Pareto improvement over X.
There are no other Pareto improvements among the outcomes in this game, just this one (D,D) (C,C).
Now let’s examine individual incentives. If you were playing, what should you do? You don’t know what your opponent will play, but you can reason about each situation in turn. If he is planning to cooperate, then you could either cooperate also, or else defect and exploit him. 2<3 so you'd best defect to exploit. If he is planning to defect, your choice is either to cooperate and be a sucker, or else defect as well. 0<1 so you'd best defect for self-defense.
Both players face the same incentives (the game is exactly symmetric). This diagram shows their preferences over outcomes they control. Remember, the row player’s payoffs are the left side of each pair, and the column player’s payoffs are the right side of each pair.
I’d like to have arrows connecting social outcomes, not individual outcomes, so let’s rewrite the diagram like so:
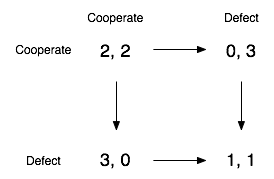
So the 
marks a selfish preference aligned with a unilateral choice; that is, X 
Y means that one player could have control over whether X or Y is picked, and he prefers Y over X. ‘s can only appear horizontally or vertically, since they represent a relationship between outcomes that only exists between outcomes whose difference is only in the decision of one player. (The difference between the diagonal outcomes (C,C) and (D,D) requires a change by both players; it is not due to a mere unilateral choice.)
Looking at the diagram, it’s clear the individual incentives are very stark: each player should defect under all circumstances. (Arrows on both left and right point down.) There is only one outcome that only has arrows flowing in and not out: D,D. If an outcome only has incoming arrows, and no outgoing ones, it is a Nash equilibrium. A way to think about it is, if both players are playing (D,D), there is no incentive for either to unilaterally switch away.
If we combine the diagrams, it’s easy to see why this is a dilemma. Individual incentives work in clear opposition to Pareto improvement! (There may be be other ethical concerns, such as the unfairness of the exploitation outcomes, but let’s put those aside for now. At the very least, this Pareto improvement seems to be a socially good thing.) The Pareto optimum is in a box, and the Nash equilibrium is circled.
Here’s a game where cooperation is a bit easier. It’s called a stag hunt, another odd name not really worth explaining. It’s similar to a PD, except the cooperation payoff is better than exploitation payoff. (In the old language, the payoff ordering is now b>a>c>d.) Let’s use numbers again — the mutual cooperation payoff is now 4 — and jump straight to the Pareto-Improvement + Unilateral-Selfish-Choice diagram:
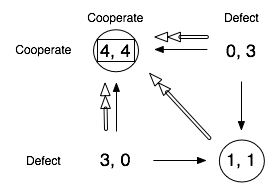
Now that mutual cooperation beats exploitation, the (C,C) outcome is now a Nash equilibrium, in addition to being Pareto superior over (D,D). (There are also two new Pareto improvements from C,D and D,C, just for kicks.) Now, with two NE’s on the table, it’s not clear what you should do if you were a player. If you were absolutely certain your opponent was going to defect, you should defect too just like in the PD. But if you thought he was going to cooperate, you should cooperate as well.
If both sides can coordinate their moves, then they can positively benefit at the superior and maintainable (C,C) outcome.
Whew, I think that’s it for now. I confess that I rather like diagramming out the incentive and payoff relationships between outcomes; I find it far more informative and instructive compared to staring at the arithmetic/algebraic tables and trying to figure it out in my head. Maybe I’m just not good enough at math.
To give credit where credit is due, I’ve seen the unilateral-selfish-choice arrows in only one place, Jim Fearon‘s excellent lecture notes, though he is not to blame for all this new crap I threw in. The arrows get really useful if you start working with games that have more than 4 outcomes, since as long as the game is discrete and you can lay out the outcomes in two dimensions, you usually can draw a bunch of graph edges between them. These diagrams can be completely formalized as much as the arithmetic algebra standardly used for game theory, since the visual graph over outcome nodes is just a way to writing down a set of binary relations on outcomes, and the row/column alignment stuff is just a way of showing how those relations interact with individual choices. You can easily imagine adding more arrows for different social preference functions, for elements of different solution concepts, etc.
Some people have done work with the taxonomy of 2×2 games; it might be useful to illustrate the differences (e.g. pure coordination versus pure conflict games) as outcome graph diagrams. Another post I guess…
