Lately, I’ve been trying to memorize very small tables, especially for better intuitions and rule-of-thumb calculations. At the moment I have these above my desk:
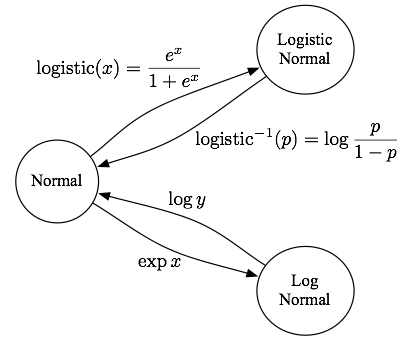
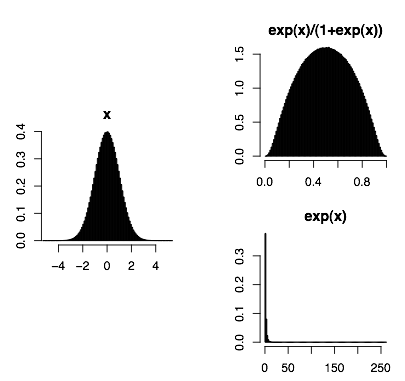
The first one is a few entries in a natural logarithm table. There are all these stories about how in the slide rule era, people would develop better intuitions about the scale of logarithms because they physically engaged with them all the time. I spend lots of time looking at log-likelihoods, log-odds-ratios, and logistic regression coefficients, so I think it would be nice to have quick intuitions about what they are. (Though the Gelman and Hill textbook has an interesting argument against odds scale interpretations of logistic regression coefficients.)
The second one are some zsh filename manipulation shortcuts. OK, this is more narrow than the others, but pretty useful for me at least.
The third one are rough unit equivalencies for data rates over time. I find this very important for quickly determining whether a long-running job is going to take a dozen minutes, or a few hours, or a few days. In particular, many data transfer commands (scp, wget, s3cmd) immediately tell you a rate per second, which you then can scale up. (And if you’re using a CPU-bound pipeline command, you can always use the amazing pv command to get a rate-per-second estimate.) This table is inspired by the “Numbers Everyone Should Know” list.
The fourth one is the Clopper-Pearson binomial confidence interval. Actually, the more useful ones to memorize are Wald binomial intervals, which are easy because they’re close to \(\pm 1/\sqrt{n}\). Good party trick. This sticky is actually the relevant R calls (type binom.test and press enter); I was using small-n binomial hypothesis testing a lot recently so wanted to get more used to it. Maybe this one isn’t very useful.